界面と表面
界面とは，気体/液体，気体/固体，液体/液体，液体/固体，固体/固体など，異なる物質の境界となる面のことです。「気体」のかわりに，「真空」であっても構いません。
このうち，気体/液体の界面，気体/固体の界面は，それぞれ，「液体の表面」，「固体の表面」という言い方のほうが一般的です。
例えば，ガラスのコップに注がれた水の表面は，厳密に言えば，空気という気体と水という液体との界面です。また，ガラスの表面は，空気という気体とガラスという固体との界面です。
コップの内側には水が入っていますが，この水とコップ内面との境界は，水という液体とガラスという固体との界面です。
このコップに，さらに油を注いでみるとどうなるでしょうか?
水と油は互い混ざり合わないことはよく知られています。また，油の比重は，水のそれよりも小さいこともよく知られています。したがって，水の入ったコップに油を注ぐと，上層には油が集まり，下層には水が集まります。このとき，油と水が分離してはっきりとした境界を作ります。この境界が，油という液体と水という液体との界面です。
液体どうしの界面は常にできるわけではありません。例えば，エタノールと水とをコップに入れてよくかき混ぜると，互いに溶解するので分離することがなく，したがって界面を作ることはありません。
他方，このコップが木製のテーブルの上に置かれているとすれば，このコップとテーブルとの境界は，ガラスという固体と木材という固体との界面ということになります。
このように，界面はいたるところに存在し，様々な現象に深く関わっています。
液体/固体界面でみられる現象の代表的なものは「ぬれ」です。
ぬれの良否は，いいかえれば，液体と固体との相性の良否ということになりますが，これは結局，液体，固体それぞれの性質が反映されたものということになります。したがって，ぬれの良否は，固体の表面の付着性，離型性，防汚性などとも密接に関連しています。
例えば，テフロンなどの商品名で知られるポリテトラフルオロエチレン（PTFE）の表面は水をはじきますが，ほかの固体と接着もしにくく，逆に離型材として利用されています。
ぬれは，普段，意識することはあまりないかもしれませんが，日常生活ではいたるところでみられる現象です。
例えば，買ってきたばかりのきれいなコップの表面は，水でよくぬれます。しかし，何度も使ったコップの表面は，たとえそれが都度洗ったものであっても，いつの間にかぬれが悪くなっています。
ガラスは本来，親水性の（水になじみやすい）表面をもっていますから，きれいな状態であれば，水でよくぬれます。しかし，使い込んでいくと，毎回きれいに洗ったつもりであっても，洗い残しの微量の油分がガラスの表面に少しずつ蓄積されます。そうすると，水と油は仲が悪いので，水をはじくようになります。
このほかにも，様々なぬれの現象があります。
このようなぬれの良否，すなわち，ぬれ性を表現するときに，一般的には，「ぬれがよい（はじきが悪い）」，「ぬれが悪い（はじきがよい）」というような表現が用いられます。
ぬれ性を判断する簡単な方法の一つは，固体表面上の液滴形状を水平方向からを観察することです。固体表面に対して，液滴が広がっていれば「ぬれがよい」ということになり，一方，丸まっていれば「ぬれが悪い」ということになります。
しかし，ぬれがよい，悪いというような表現は感覚的なものであり，その基準は人によって異なります。これでは，客観性が求められる科学技術の世界では困ったことになります。
そこで，接触角という量によって，ぬれ性を定量的に表現します。
接触角は，下図に示すような角度θで表され，0°から180°までのいずれかの値をとります。下図の点線は，液滴の輪郭曲線と固体表面との交点における，輪郭曲線の接線を表しています。
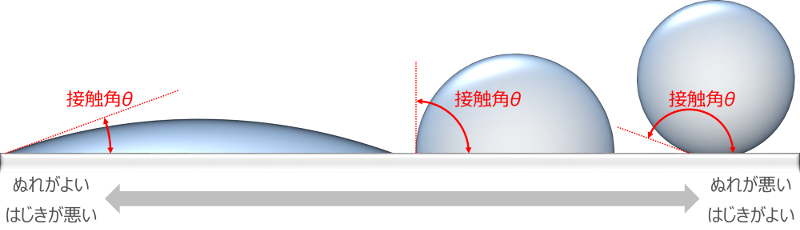
接触角θが0°に近いほど，「ぬれがよい」ということになり，一方，接触角が180°に近いほど「ぬれが悪い」ということになります。
例えば，清浄なガラス表面を水がぬらす場合は，水はガラス面上で広がることになり，接触角は10°以下となります。一方，ポリテトラフルオロエチレン（PTFE）のようなフッ素系材料の表面に置かれた水滴の場合には，水滴は丸まるようになり，接触角は120°以上になることもあります。
このように，接触角という概念を利用すれば，ぬれの状態を0°から180°までの角度の値で直感的かつ客観的に表現できるようになります。
固体表面が水にぬれやすい場合，その固体は親水性であるといい，逆に水をはじく場合は撥水性であるといいます。
親水性/撥水性の区分は相対的なものですが，接触角が90°以下か90°以上かということによって親水性/撥水性が区分されることもあります。さらに接触角が5°以下で超親水性，150°～160°以上になると超撥水性といわれることもあります。
光触媒などを利用した超親水性材料では，接触角はほぼ0°になり得ます。一方，超撥水材料では，2013年には接触角が179.8°という報告も出ています。
なお，固体表面が油にぬれやすい場合は親油性，油をはじく場合は撥油性といいます。
このような液体と固体とのぬれの現象はどのようにして決まるのでしょうか?
ぬれ性，すなわち接触角θを支配しているものは液体，固体それぞれの表面張力γL，γS，及び液体/固体間の界面張力γLSのバランスです。
この関係は，後述する次のYoungの式としてよく知られています。
では，表面張力とは何でしょうか?
コップの縁すれすれのところまで水を注ぎ，さらにゆっくりと注いでいくと，水面が盛り上がります。この現象が表面張力によるものであることはよく知られています。
この現象をもう少し深く考えてみましょう。
水には質量がありますから，地球上では重力がはたらきます。
重力には，物体の位置をできるだけ低いところに保とうとする作用があります。
例えば，ボールを斜面に静かに置いて手を離すと，そのボールは斜面をひとりでに転がり落ちていきます。これは重力の作用によるものです。逆に，このボールが，斜面をひとりでに登っていくことはありません。
さて，水をゆっくり注いで水面の高さが徐々に高くなっているときにも，重力は常に作用しています。したがって，注がれた水は，その水面の高さができるだけ低くなるような位置にとどまろうとします。このとき，コップの中には水が満たされていて水の行き場はないので，注がれた水の水面の高さをできるだけ低く保つためには，その水がコップの縁からこぼれてしまうしかありません。
この状態は，重力が水面を上方から押さえつけていると考えてもよいでしょう。
しかし実際には，水を注いでいったときに，コップの縁からすぐにこぼれるのではなく，ある程度の高さまで水面が盛り上がります。
この現象を説明するためには，水面を押さえつけようとする重力の作用に抗して，「何らかの別の力」がはたらいていると考えざるを得ません。この何らかの別の力が水の表面に作用している表面張力です。
水を注いでいったときに，水の表面張力によってある程度の高さまでは水面が盛り上がりますが，さらに注ぎ続けると水はコップの縁からこぼれてしまいます。これは，水面が高くなると，水面を押さえつけようとする重力の作用がさらに大きくなって，表面張力の作用がこれを支えきれなくなるためです。
表面張力は，水だけでなく，一般の液体の表面にも作用しています。さらに固体の表面にも作用しています。
すでに説明したように，液体の表面とは気体/液体の界面，固体の表面とは気体/固体の界面のことですから，「液体の表面張力」をもう少し正確にいえば，「気体/液体の界面にはたらく界面張力」ということになります。「固体の表面張力」も同様に，「気体/固体の界面にはたらく界面張力」ということになります。
界面はこのほか，液体/液体の界面，液体/固体の界面，固体/固体の界面がありますから，それぞれの界面には界面張力がはたらきます。
固体の表面張力や界面張力の詳細については，後述します。
さて，液体の表面張力はどのようにして発生するのでしょうか?
一般に，分子と分子との間には，分子間力とよばれる，分子どうしが互いに引き合う力が作用します。その力の大きさは，分子の種類，分子間の距離，分子の向き（配向）によって決まります。
水の固体である「氷」は，水分子の分子間力によって分子どうしが互いに引き合い，多数の分子が結合した状態です。この状態では，それぞれの水分子の位置はほとんど固定されており，ある点を中心に振動しているだけです。これが「固体」の状態です。
しかし，温度が高くなると，水分子の熱運動が激しくなり，分子は位置を変えながら，ある程度自由に動けるようになります。とはいうものの，まだまだ分子間力による引き合いの効果のほうが大きく，分子と分子がばらばらになるには至りません。これが「液体」の状態です。
さらに温度が高くなると，水分子の熱運動がさらに激しくなり，分子間力による引き合いを振り切って完全に自由に動けるようになります。これが「気体」の状態であり，水の場合は「水蒸気」とよばれます。なお，気体の状態では，分子がばらばらになっており，「表面」というものが存在しません。したがって，「気体の表面張力」という概念もありません。
このような，固体，液体，気体という「物質の3態」には分子間力が大きく関わっていますが，実は表面張力にも，分子間力が大きく関わっています。
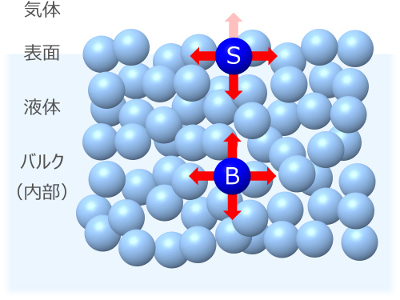いま，液体の表面付近における分子の状態を考えてみましょう（右図）。
まず，液体のバルク（内部）に存在する，ある1個の分子Bに着目します。この分子Bと，その周辺に存在するあらゆる分子との間には分子間力がはたらいています。
液体中の分子は，ほかの分子からの分子間力の作用を受けながら，ほぼ無秩序に熱運動しています。したがって，ある分子にはたらく分子間力は，大きさも向きも様々です。
分子Bにも，様々な方向から様々な大きさの分子間力がはたらきますが，ある時間（例えば1秒間）で区切ってその時間内の平均的な分子間力を考えてみると，あらゆる方向から同じような大きさの分子間力が常にはたらいていることになり，結果的にはバランスが保たれていることになります。
バランスが保たれているということは，安定しているということです。分子Bにとっては，「居心地がいい」ということになります。
一方，表面（すなわち，気体/液体の界面）に存在するある分子Sに着目すると，この分子は，両隣やバルク側の分子から分子間力の作用を受けますが，気体側の分子からはほとんど分子間力の作用を受けません。なぜなら，気体側の分子数密度は，バルク側のそれと比較して圧倒的に低いからです。
その結果，分子Sでは，分子Bのようなバランスが保たれていないので，常にバルク側（内部）に引き込まれることになります。このような現象が，表面のいたるところで起こっています。
したがって，分子Sのような表面の分子は，分子Bのようなバルクの分子と比べて不安定であるといえます。分子Sにとって，表面にとどまり続けることは，とても居心地が悪いことなのです。
見方を変えれば，表面に存在している分子は，それ自身の居心地が悪いために，居心地のよさを求めて常にバルクに潜り込むように再配列しようとしています。その結果，液体の表面積をできるだけ小さくしようとする傾向が現れます。すなわち，表面には，その表面積を小さくするような「張力」がはたらいていることになります。これが「表面張力」です。
ところで，液滴の体積が一定であれば，表面積が最小となる形状は球です。
宇宙空間のような無重力状態では，液滴に対して重力の作用はありません。したがって，表面張力以外の外力が作用しなければ，液滴の形状は完全な球状になります。なぜなら，液滴表面にはたらく表面張力が，できるだけ表面積を小さくしようとするからです。
地球上のように重力が作用する場合はどうでしょうか?
液滴の体積が十分に小さいうちは，その質量も小さいので，重力の作用よりも表面張力による作用のほうが支配的になります。したがって，液滴形状は球に近くなります。
しかし，液滴の体積が大きくなると，その質量も大きくなり，重力の作用が支配的になってきます。したがって，液滴形状は潰れてきます。実際，バケツに入った数リットルの水を床にぶちまけたとしても，直径数十センチメートルの球状の液滴ができることはありません。その水は，高々，数ミリメートルのある「厚み」をもって床面に広がります。ただし，このことは，水と床面とのぬれがいいかどうか，すなわち，接触角が0°に近いかどうかとは別の話です。バケツの水が床面に広がったとしても，床面の材質が撥水性の高い材料でできていれば，接触角は90°以上になるはずです。
さて，分子間力の大きな液体というのは，それ自身の凝集力が大きいということを意味します。これは，表面の分子をできるだけバルク側に移動させて表面積を小さくしようとする作用が大きいということですから，結果的に，その液体の表面張力も大きくなります。
固体に対するぬれという観点で考えると，液体の表面張力が大きいほど，それ自身が広がるよりも凝集して丸まろうとする傾向が強く，固体表面に対してぬれにくいということになります。
表面張力は「表面の単位長さにはたらく力」として定義され，「力/長さ」の次元をもつ量です。単位は通常mN/m（ミリニュートン毎メートル）が用いられます。例えば水の表面張力は72.8mN/m（20℃）です。
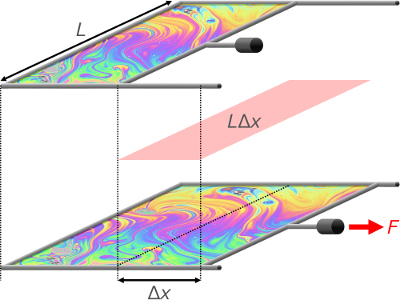
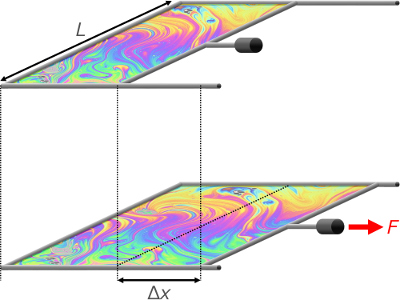単位長さにはたらく力としての表面張力は，Maxwellの枠といわれる，右図のようなモデルを考えれば理解しやすいでしょう。
コの字型の枠に，自由に動かせる仕切り棒をつけておき，それらで囲まれた部分に石けん膜のような液体膜を張ります。
この膜の表面には表面張力がはたらき，膜の表面積を小さくしようとします。したがって，膜を広げる，すなわち，仕切り棒を右側に動かすためには，表面張力の作用に抗するための力Fが必要です。膜の幅Lが2倍，3倍，・・・になれば，分子間力に由来して発生する表面張力の作用も2倍，3倍，・・・になると考えられますから，力Fは膜の幅Lに比例することになります。
ただし，膜には表/裏があり，それぞれの表面に表面張力がはたらきます。このことを考慮すると，膜の幅は，表/裏を考慮して，2L相当の長さとしておかなければなりません。
つまり，Maxwellの枠で膜を広げるのに必要な力Fは，膜の表/裏を考慮した幅2Lに比例するということになります。このときの比例定数をγとすれば，次のように表すことができます。
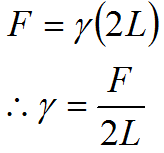
これが表面張力の定義です。力を長さで割っており，表面張力が「表面の単位長さにはたらく力」であることがわかります。
先述のように，バルク分子にはあらゆる方向から同じような大きさの分子間力が常にはたらいており，安定しています。これは，バルク分子は，周辺分子と相互作用することにより，エネルギーを下げて安定な状態になっているとみることができます。
一方，表面分子は，気体側に相互作用できる相手分子が少ないため，エネルギーを下げて安定化することができません。このため，バルク分子と比較すると，その分だけエネルギーが高く，不安定な状態になっているとみることができます。
言い換えると，表面は，バルクよりも過剰なエネルギーをもっているということになります。この過剰なエネルギーのために，表面はバルクよりも不安定になっているのです。この過剰なエネルギーを単位面積あたりの表面の量としてとらえたものが表面自由エネルギーとよばれるものです。
すでに出てきたMaxwellの枠を使って，表面自由エネルギーを物理的に定義してみましょう。
Maxwellの枠で，液体膜の表面積を広げるためには，仕切り棒を右側に移動させる必要があります。そのためには右向きの力Fが必要です。なぜなら，液体膜の表面張力が，膜の表面積を小さくしようとするからです。
仕切り棒に力Fを加えつつ，その方向にΔxの距離だけ移動させたとすれば，この力は仕事をしたことになります。この仕事をWとすれば，Wは次式で表されます。
この力Fを表面張力γを使って表すと，次式のようになります。
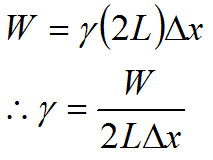
右辺の分母の2LΔxは，仕切り棒を引っ張ることにより増加した液体膜の表面積（ただし，表/裏の合計）に相当します。
この式で表されるγを右辺の量に基づいて解釈すれば，「液体膜の表面積を増加させるのに必要な，単位面積あたりの仕事」ということになります。
表面の面積を増加させるためには，バルク分子を移動させて表面に配置しなければなりません。このとき，分子の凝集力（つまり分子間力）に抗して分子を移動させる必要があるので，外部から「仕事」をしなければなりません。この仕事の単位面積あたりの量がγとなります。そして，このγに相当するエネルギーが単位面積の表面に蓄えられることになります。
これは，物体をある高さに持ち上げるためには，外部から仕事をする必要があり，その仕事に相当する分のエネルギーが物体の位置エネルギーとして蓄えられるのと同じです。
さて，液体膜の表面積の増加が，温度一定の条件下で可逆的になされるとすれば，仕事Wは，増加した部分の表面に「エネルギー」としてまるまる蓄えられることになります。このエネルギーは逆に，仕事として，まるまる取り出すことができます。つまり，熱力学的な意味で，「自由に」取り出すことができます。
したがって，温度一定の条件下で，外部からなされた仕事Wによって液体膜の表面に蓄えられたエネルギーは，「自由エネルギー」ということになります。それを単位面積あたりの量としてとらえたものが「表面自由エネルギー」です。
なお，ここでは深くは立ち入りませんが，「表面エンタルピー」の意味で「表面エネルギー」という用語が用いられることもありますので，「表面自由エネルギー」のことを簡約して「表面エネルギー」とはいわないほうがよいでしょう。
このように，表面自由エネルギーは「表面の単位面積がもつ自由エネルギー」として定義され，「エネルギー/面積」の次元をもちます。単位は，通常mJ/m2（ミリジュール毎平方メートル）が用いられ，例えば水の表面自由エネルギーは72.8mJ/m2（20℃）です。
表面張力と表面自由エネルギーは，物理量として等価な次元をもつ量であり，同じ単位系で表せば，数値も等しくなります。例えば水の場合，72.8mN/m=72.8mJ/m2となります。
ただし，力としてとらえる表面張力は，ベクトル量であり，力としての向きを考慮する必要があります。エネルギーとしてとらえる表面自由エネルギーは，スカラー量であり，向きという概念はありません。
さて，表面張力が大きいということは，その表面積を小さくしようとする作用が大きいことを意味しますが，これは，エネルギーという観点から考えると，次のようになります。
ある液体の表面がもつ表面張力をγ（mN/m）とすれば，これはその液体の表面自由エネルギーがγ（mJ/m2）であることと同じです。すなわち，この液体の表面は単位面積あたりγという一定のエネルギーをもつので，表面積が小さくなったほうが，「表面全体」のもつ自由エネルギーが小さくなって，安定になるということを意味しています。
地球上では重力の作用もあります。これは位置エネルギーとして加味しなければなりません。固体表面上に置かれた液滴や，下向きの細管にぶら下がる液滴（懸滴）では，重力による位置エネルギーも含めて，全体の自由エネルギーが最小になるような液面形状になります。
先述のとおり，固体にも表面張力があります。
固体も液体同様に原子，分子から構成されています。したがって，固体表面でも，液体同様に分子間力のアンバランスが生じ，その表面積（気体/固体界面の面積）をできるだけ小さくしようとする傾向が出てきます。
エネルギーという観点でみれば，固体表面にも，表面自由エネルギーがあるということです。
ただし，固体を構成する分子は，液体分子ほどには自由に動けません。したがって，自らの分子を再配列させて表面積最小の形状に変形するというのは容易ではありません。
そこで，自らの分子の再配列によるよりも，気体，液体，微粒子を吸着したり，ほかの固体と付着することによって，自らの表面積（気体/固体界面の面積）を小さくし，安定化を図ろうとします。
したがって，固体の表面自由エネルギーが大きいほど，気体や微粒子を吸着しやすく，液体でぬれやすく，ほかの固体と付着しやすくなります。
固体どうしの接着の例で考えてみましょう。
固体どうしを接着するには，通常，接着剤を使います。接着剤の注意書きには，接着面の汚れをよく拭き取るように書いてあります。これはどういうことでしょうか?
固体表面は，常にそのエネルギーを下げようとしていますので，空気中の微粒子などが近くにあれば，それを吸着してエネルギーを下げ，安定化します。こうして固体表面に吸着したものが「汚れ」です。
言い換えれば，汚れている表面というのは，すでにその表面のエネルギーが低下して，安定化しているということであり，ほかの固体と付着（接着）する能力が落ちているということになります。
そこで，汚れを除去すれば，エネルギーの高い本来の表面が復活し，ほかの固体と付着（接着）する能力が高まるということです。
逆に防汚性，撥水性，離型性を狙う場合には，固体の表面自由エネルギーを小さくすればよいということになります。このような場合に，フッ素系材料のコーティングなどが施されますが，これはフッ素系材料のエネルギーが小さいことを利用しているのです。
エネルギーの高い表面を人間社会にたとえるならば，エネルギッシュな人が社交的で誰とでもすぐに仲良くなれるのと同じです。
他方，エネルギーの低い表面は，それだけで十分に安定しているので，気体や微粒子を吸着したり，液体でぬれたり，ほかの固体と付着する必要がないのです。これは物静かな人が孤独を愛するのと通ずるかもしれません。
先述のとおり，液体の表面張力，固体の表面張力はそれぞれ，気体/液体の界面にはたらく界面張力，気体/固体の界面にはたらく界面張力ということになります。
このほか，液体/液体，液体/固体，固体/固体の各界面には界面張力がはたらきます。
界面では，その界面の両側にはたらく分子間力のアンバランスによって不安定な状態になっています。そのため，界面の面積をできるだけ小さくしようとする傾向が生じます。これが界面張力です。 表面張力/表面自由エネルギーの場合と同様に，界面の単位面積がもつ過剰なエネルギーが界面自由エネルギーであり，これは界面張力と等価です。 界面張力（界面自由エネルギー）が小さいということは，その界面が安定であることを意味します。
前節で，固体の表面自由エネルギーが大きいほど，気体や微粒子を吸着しやすく，液体でぬれやすく，ほかの固体と付着しやすくなると述べましたが，そうすると，固体自らの表面積（気体/固体界面の面積）が小さくなる代わりに，吸着層/固体の界面，液体/固体の界面，固体/固体の界面の面積が増加することになります。界面の面積が増加すれば，その分だけ，不安定さも増加することになります。
したがって，全体としては，固体自らの表面積の減少分と，新たにできた界面の面積の増加分とを加味して，どういう状態になるのが最も安定になるのかということが重要になります。
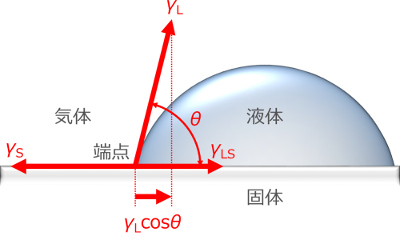液体と固体とのぬれを再び考えてみましょう。
固体表面上の液滴形状を水平方向からを観察したときに，液滴の輪郭曲線と固体表面との交点を「端点」とすれば，端点における接触角が右図のθです。
このとき，端点には，固体の表面張力（気体/固体間の界面張力）γS，液体/固体間の界面張力γLS，液体の表面張力（気体/液体間の界面張力）γLがはたらきます。
固体の表面張力γSは，固体の表面，すなわち，気体/固体間の界面の面積を小さくしようとして，端点を左側に引っ張ります。
液体/固体間の界面張力γLSは，液体/固体間の界面の面積を小さくしようとして，端点を右側に引っ張ります。
液体の表面張力γLは，液体の表面，すなわち，気体/液体間の界面の面積を小さくしようとして，液滴輪郭の接線方向にはたらきますが，その水平方向の成分γLcosθが端点を右向きに引っ張ります。
ぬれの状態が安定しているとき，端点は右にも左にも動かず，静止していますから，これらの3つの力はつり合っていることになります。
この3つの力のつり合いを示したものが次のYoungの式です。
ぬれの良否は，分子の立場でいうと，液体分子どうしで集まっているのが安定（居心地がよい）なのか，それとも，液体分子が固体分子に寄り添ったほうが安定なのかということが反映されたものです。
したがって，ぬれ性，すなわち接触角の大小は，液体と固体それぞれの表面特性によって決まることになります。このことは，Youngの式を次のように変形するとわかりやすいでしょう。
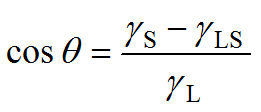
cosθが大きくなって1に近づくということは，接触角θが0°に近づき，ぬれがよくなることを意味しますから，ぬれをよくするための方法は，（1）液体の表面張力γLを小さくする，（2）固体の表面張力γSを大きくする，のいずれかです。
この式では，cosθはγL，γS，γLSの3つの独立なパラメータで決まるようにみえますが，実は，γL，γSが決まるとγLSが自動的に決まります。詳細は表面張力（表面自由エネルギー）の成分分けという概念を導入して議論する必要がありますが，ここでは割愛します。
ぬれをよくするために，液体に界面活性剤が添加される場合がありますが，これは界面活性剤が液体の表面張力を下げるという作用を利用したものであり，方法（1）に相当します。
一方，固体表面を化学的あるいは物理的に改質してぬれをよくする場合は，方法（2）に相当します。
このように，ぬれ性，すなわち，接触角を決めている因子はあくまでも液体と固体それぞれの表面張力です。
つまり，液体と固体の表面の性質が決まれば，液体，固体それぞれの表面張力（表面自由エネルギー）が決まります。その結果として，液体/固体界面の界面張力（界面自由エネルギー）が決まり，これらのバランスによって最終的にぬれ性が決まるということになります。
ある固体に対する気体・微粒子の吸着や，固体どうしの付着（接着）の場合も考え方は同じです。それらが単独で存在していたほうが安定なのか，界面を作って存在したほうが安定なのかということによって，吸着のしやすさや付着のしやすさが決まります。